This week in class the concept of mathematical classroom equity was introduced, which is a concept that immediately elicited my attention. I have often contemplated the idea of equity, but in the concept of equity vs. equality. It was a topic introduced to me a while ago when I found this image:

At the time I was considering the argument of equity vs. equality in a political sense, because in our current political climate many groups campaign for equality when they really wan equity. I had not thought about it in an educational sense.
So, when the topic came up in class that we would be looking at Case Studies and deciding whether they were equitable or not, I was immediately interested. My main item of discussion and knowledge for equity in the classroom comes from our assigned reading of chapter two Equitable Mathematics Teaching from Strength in Numbers Collaborative Learning in Secondary Mathematics by Ilana Seidel Horn. URL: https://drive.google.com/file/d/0B1zVoWMFl08-TGN2NWxQMXVPVGc/view
I found the chapter intriguing to read and took out many good points and concepts from it. The first thing is how the book defines equity in math as “equitable mathematics teaching involves using models of instruction that optimally support meaningful mathematical learning for all students.” Meaning that teachers should be using a variety of methods and techniques in order to reach students of various learning styles.
The second thing I found most helpful was the three practices they listed for collaborative learning environments that influenced equitable math teaching.
- What counts as math involves how mathematics is presented to students and the messages about what success means.
- Pedagogical practices focus on the work of teaching.
- Relational practices address the relationships that students build with others in the school and classroom.
Finally, the four principles for equitable math teaching where:
- Learning is not the same as achievement.
- Achievement gaps often reflect gaps in opportunities to learn.
- All students can be pushed to learn mathematics more deeply.
- Students need to see themselves in mathematics.
There are many things here that I would love to implement into my own classroom. Like, using group based work in order to help build the classroom as a community of learners so that way they feel part of a collaborative effort. They could take on a role in their team that meets their strong suit. Also, having across classes activities. That is to say, the algebra students work on the calculations to some 3-dimensional shapes the geometry students are making. That way they feel more connected as a school.
Having students see themselves as mathematicians is also so important. I am a firm believer that everyone can do math, because it is a universal language that can be taught in many different ways. If one way is not working for a student, then it should be I as a teacher to make my classroom equitable so that that student can find a way that helps them learn math. Every student deserves a fair opportunity to learn such that they can be at the same level as all of their peers. Constantly berating students with quizzes, homework, and tests when they are doing poorly does not mean they are going to learn math. Students learn math in many different ways, but they can all learn math.
After learning more about equability in education I like to see equity more like this:

After learning all this information about how I can make my classroom equitable, I wanted to be able to see it in action. What are the different ways equity can be incorporated? So, I went to the National Council of Teachers of Mathematics and found this video that showed me a lesson of how a teacher used equity in her math classroom. URL: http://www.nctm.org/Conferences-and-Professional-Development/Principles-to-Actions-Toolkit/Equitable-Pedagogy/
In the video the students are learning about finding the area of a square, and they all have to go to the board to present how they found their area. They are all in partners by the looks of it, and the partner groups have varying degrees of difficulty in their square. What I mean by this is some students have a regular square that has a flat side on the bottom, but other students have their square skewed so a corner is touching the bottom. Like this:
The students who may struggle more would be given the square on the left so they could count the grids from top to bottom and left to right then multiply to find the area. While the students who understand it more get the square on the left where they have to combine the areas of a square and triangle to find the total area. This way both groups of students are given materials at their level of understanding.
Finally, in the video you can see a great example of peer collaboration. When two students with the harder square are at the board presenting, one student asks them how they got the area of their triangle. This forces the two students presenting to explain their rational, allowing the teacher to check their thinking, and the student who asked the question gets to learn something new.
One adjustment I would make to an equitable classroom would be to find a better way to mix students at the upper end and lower end of the class to see how further growth and understanding could be resulted from that. Right now, to me, it seems like equity is giving the “smarter” kids material for deeper understanding and other students material to try to reach the “smarter” kids. Equity has been an interest of mine for a while now, and I am excited to learn more about how to implement it into my future classroom.


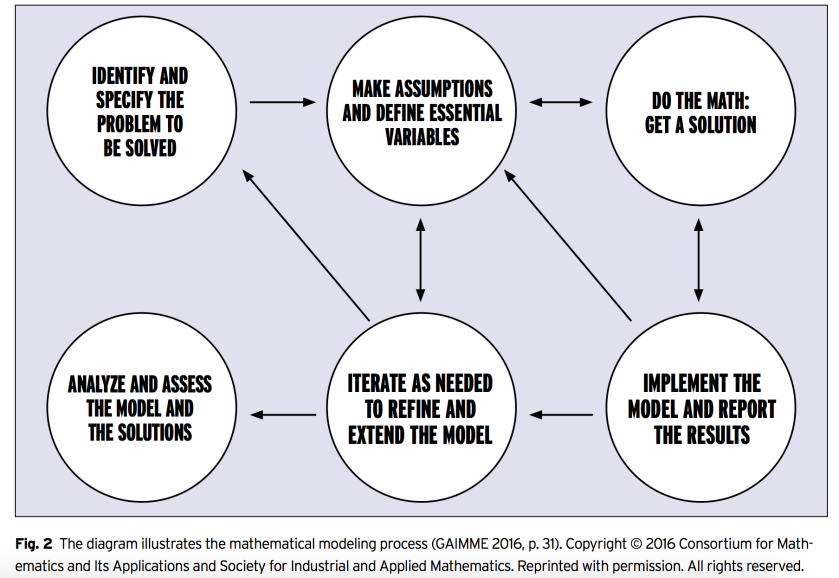 It asks students to perform tasks similar to that of PBL, but from the description in the article, modeling should take place over one to two class periods. The concept of modeling in itself asks students to apply their learning to real-world situations, deepening their understanding of the material. A portion of the article focuses on the teacher’s role in modeling. It addresses questions that the teacher should be asking him/herself before the lesson begins, such as what other resources students may need access to in order to properly address the question that the model gives the students. This indicates the preparation that should go into preparing a modeling activity for the students in the classroom. The article prompted me to consider how much of an influence giving students the opportunity to integrate their learning into real world problems can have on their learning. At the end of the article, a is quoted who describes her appreciation for having the opportunity to model in her mathematics classroom because it helped her to “remember the math.” Modeling gives students to apply what they have learned in their classes outside of the classroom, as they will eventually do as adults.
It asks students to perform tasks similar to that of PBL, but from the description in the article, modeling should take place over one to two class periods. The concept of modeling in itself asks students to apply their learning to real-world situations, deepening their understanding of the material. A portion of the article focuses on the teacher’s role in modeling. It addresses questions that the teacher should be asking him/herself before the lesson begins, such as what other resources students may need access to in order to properly address the question that the model gives the students. This indicates the preparation that should go into preparing a modeling activity for the students in the classroom. The article prompted me to consider how much of an influence giving students the opportunity to integrate their learning into real world problems can have on their learning. At the end of the article, a is quoted who describes her appreciation for having the opportunity to model in her mathematics classroom because it helped her to “remember the math.” Modeling gives students to apply what they have learned in their classes outside of the classroom, as they will eventually do as adults. 



